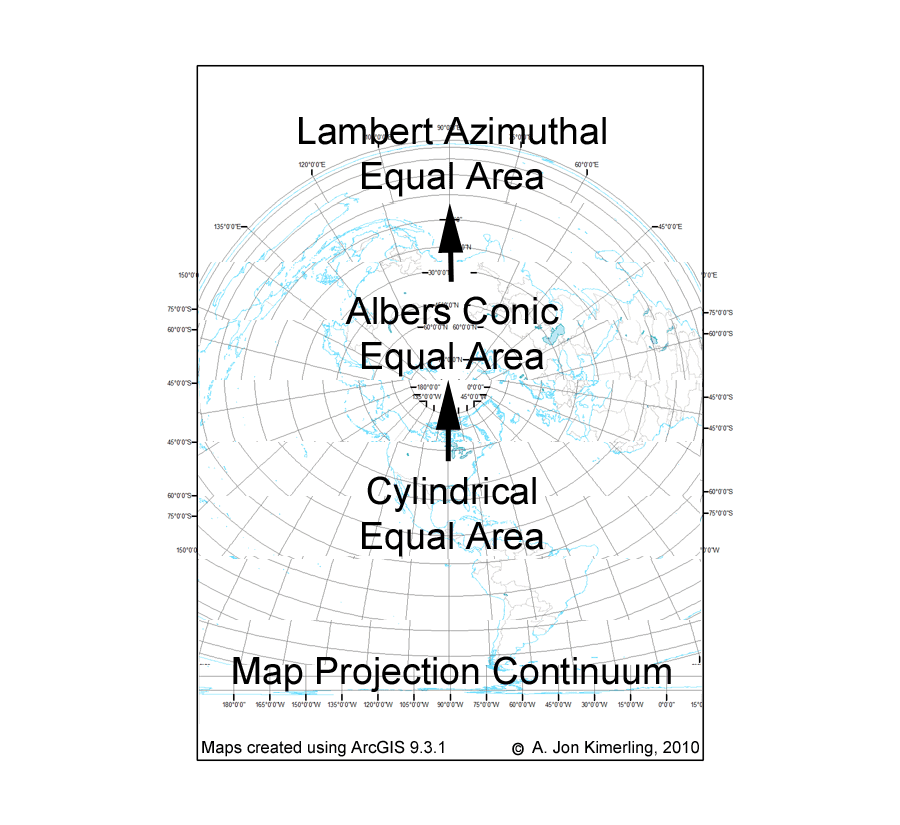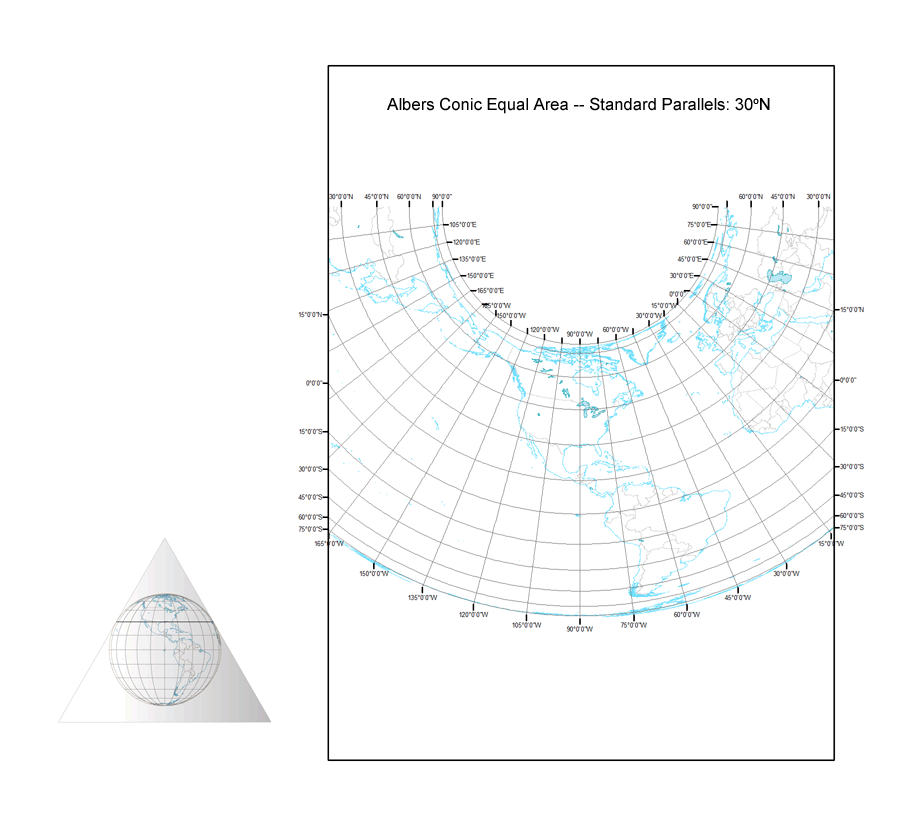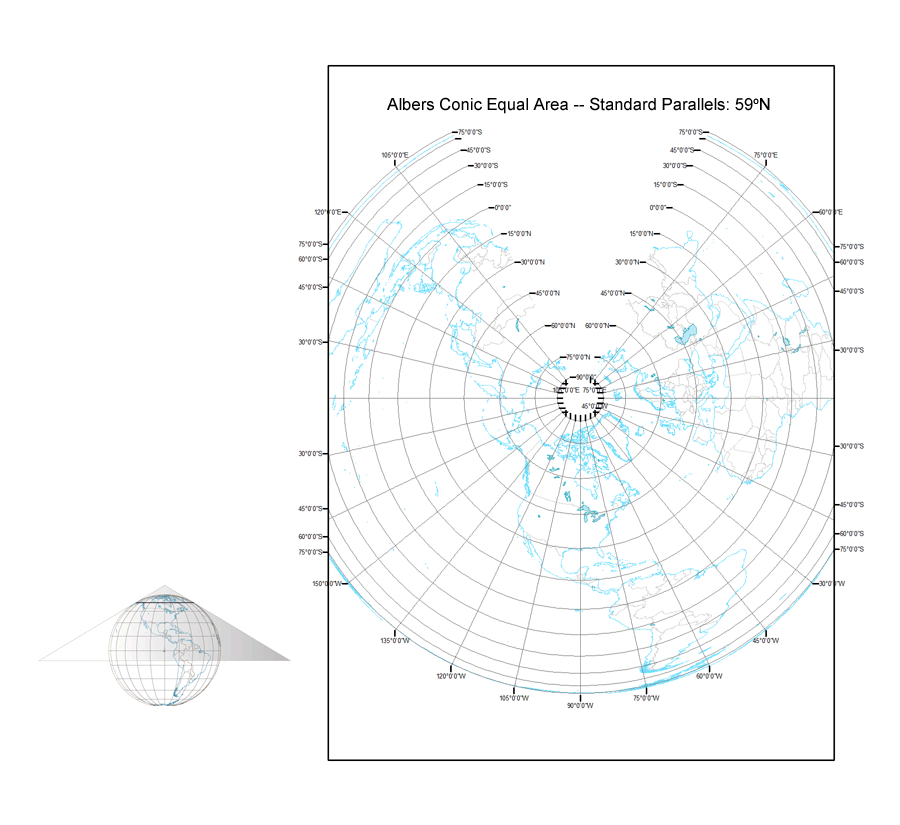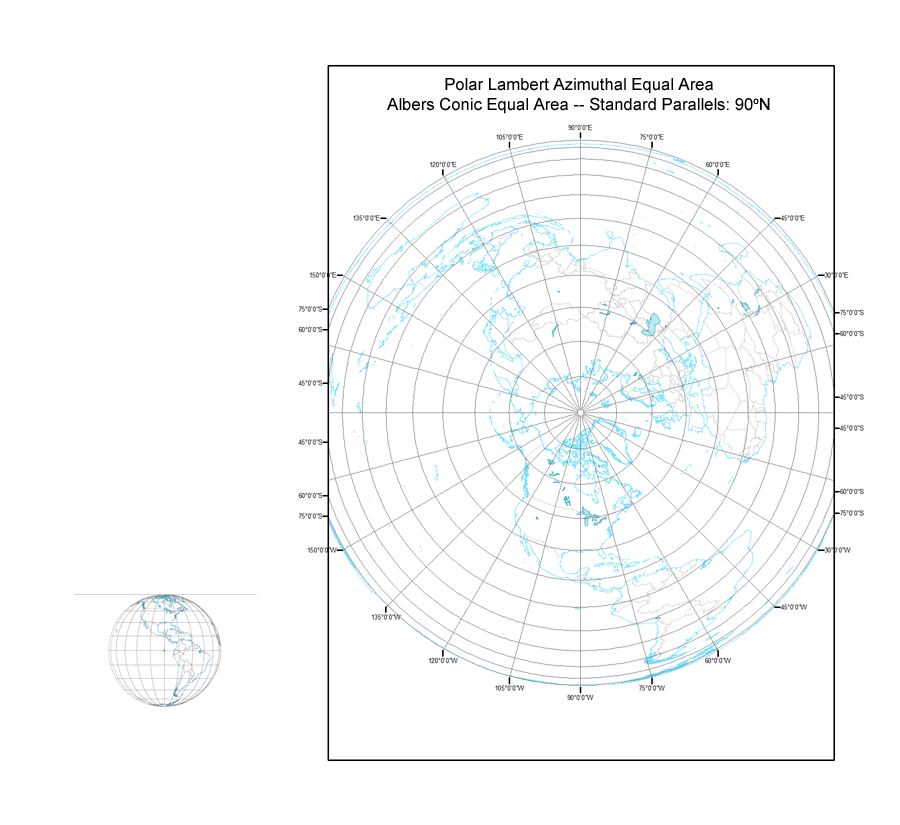
Albers Continuum Thumb

Full size [1Mb] US Soils Taxonomic Order Map

There are many ways that we can think about similarities among map projections. We can group projections as similar in map scale or as serving similar user communities. Cartographers often take a different approach and group projections by similar geometrical properties or by similar mathematics underlying their construction. Grouping projections into cylindrical, conic, and azimuthal classes is an example of grouping by similar geometrical properties, whereas categorizing projections as conformal, equal area, and equidistant is an example of grouping by similar distortion properties that are a consequence of the mathematics underlying the projections.

In this blog I would like to introduce another way of thinking about similarities among projections -- that seemingly distinct projections may actually be parts of a continuum of projections created by varying the parameters of a single pair of projection equations transforming latitude and longitude coordinates on the sphere or ellipsoid into (x,y) Cartesian coordinates on the flat projection surface. Such projection continuums are best illustrated by animations that show the changes in the graticule and coastline as a certain projection parameter is varied systematically through a large range of values. The seven map projection continuums described in the following paragraphs can be downloaded by clicking on the image to see it at full size, then right clicking and selecting "Save". I hope you will find these animations useful in your quest for further understanding the nature of map projections.


<< A really neat illustration of how the several projections warp the world for localized purpose >>